Chapter 7 Cluster Analysis

While classification looks to assign observations to pre-specified categories using predictive modelling from apriori training data, cluster analysis looks to assign observations to categories without any apriori knowledge. In this chapter we will look at several approaches to the detection and analysis of clusters. We start by developing a methodology based upon measures of dissimilarity (‘pseudo-distance’, if you like) between multivariate observations.

7.1 Dissimilarity Matrices for Multivariate Data

Let $x_{ij}$ be the observed value of the $j$th variable for the $i$th individual (where $i=1,\ldots,n$, $j=1,\ldots,p$). A dissimilarity (or proximity) matrix $\Delta$ is an $n\times n$ matrix with element $\delta_{st}$ being the dissimilarity between individuals $s$ and $t$. The dissimilarities satisfy:

$\delta_{ss} = 0$ for all individuals $s$.
$\delta_{st} \ge 0$ for all $s, t$.
$\delta_{st} = \delta_{ts}$ for all $s, t$.

Some examples of dissimilarities include the following.

Euclidean Distance

Defined by \[\delta_{st} = \sqrt{\sum_{j=1}^p (x_{sj} - x_{tj})^2}.\] (Often average Euclidean distance preferred, when above is divided by $p$.) Suitable when all variables are numeric.

Manhattan Distance

Defined by \[\delta_{st} = \sum_{j=1}^p | x_{sj} - x_{tj} |.\] (Often average Manhattan distance preferred, when above is divided by $p$.) Suitable when all variables are numeric.

Simple Matching Coefficient

The simple matching coefficient is a similarity measure for categorical variables, given by \[\gamma_{st} = p^{-1} \sum_{j=1}^p {\bf 1}[x_{sj} = x_{tj}]\] where ${\bf 1}[A]$ is the indicator for the event: \[{\bf 1}[A] = \left \{ \begin{array}{ll} 1 & A \mbox{ occurs}\\ 0 & \mbox{otherwise}. \end{array} \right .\] The corresponding dissimilarity is \[\begin{aligned} \delta_{st} &= 1 - \gamma_{st}\\ &= p^{-1} \sum_{j=1}^p {\bf 1}[x_{sj} \ne x_{tj}].\end{aligned}\]

Note: for binary data, average Manhattan distance and simple matching coefficient give same dissimilarity.

Jaccard Coefficient

The Jaccard cofficient is a similarity measure for binary variables, given by \[\gamma_{st} = \frac{\sum_{j=1}^p {\bf 1}[x_{sj} = x_{tj} = 1]} {\sum_{j=1}^p {\bf 1}[x_{sj} + x_{tj} > 0]}.\] The corresponding dissimilarity is \[\delta_{st} = 1 - \gamma_{st}.\]

Note that $\gamma_{st}$ is the proportion of variables on which the individuals are matched once the variables on which both individuals have a 0 response is removed. This is a very natural measure of similarity when 1 represents presence of a rare characteristic, so that the vast majority of individuals have 0 responses on most most variables. In that situation, 0-0 matches provide almost no useful information about the similarity between individuals. We therefore omit these matches.

Gower’s dissimilarity

Gower’s dissimilarity was the metric used to identify nearest neighbours in the kNN() function from VIM, which we discussed in 3.4. To compute Gower’s dissimilarity we first divide any numeric variable by it’s range (to ensure all variables have range 1), and then use Manhattan dissimilarity. For categorical variables we use simple matching. Gower’s distance is then the combination of these: \[\gamma_{st} = \frac{1}{p_n}\sum_{j=1}^{p_n} \frac{|x_{sj} - x_{tj}|}{r_j} + \frac{1}{p_c} \sum_{j=1}^{p_c} {\bf 1}[x_{sj} = x_{tj}].\] where $p_n$ is the number of numeric predictors, $r_j$ the range of the $j$-th numeric variable, and $p_c$ the number of categorical predictors.

The R command for computing a dissimilarity matrix is

dist(my.data, method=..., ...)

where

my.data is a data frame (or matrix, with variables as columns).
method can be
- euclidean (In R, total distance, not average).
- manhattan (In R, total distance, not average).
- binary – the Jaccard dissimilarity coefficient.

7.2 Hierarchical Clustering

Cluster analysis in statistics is a procedure for detecting groupings in data with no pre-determined group definitions. This is in contrast to discriminant analysis, which is the process of assigning observations to pre-determined classes⁶².

Agglomerative hierarchical clustering uses the following algorithm.

Initialise by letting each observation define its own cluster.
Find the two most similar clusters and combine them into a new cluster.
Stop if only one cluster remains. Otherwise go to 2.

To operate this algorithm we need to define disimilarities between clusters. Options include:

Single linkage:: Let $\delta_{AB}$ denote dissimilarity between clusters $A$ and $B$ using single linkage. Then \[\delta_{AB} = \min \{ \delta_{st}: \, s \in A, \, t \in B \}.\]
Complete linkage:: \[\delta_{AB} = \max \{ \delta_{st}: \, s \in A, \, t \in B \}.\]
Average dissimiliary:: \[\delta_{AB} = n_A^{-1} n_B^{-1} \sum_{s \in A} \sum_{t \in B} \delta_{st}\] where $n_A$ and $n_B$ are number of members of clusters $A$ and $B$ respectively.

Example 7.1 Dissimilarities Between Clusters

Suppose that the dissimilarity matrix for 4 individuals \[\Delta = \begin{array}{cc} & 1~~~~~2~~~~~3~~~~~4\\ \begin{array}{c} 1\\ 2\\ 3\\ 4 \end{array} & \hspace{-6pt} \left ( \begin{array}{rrrr} 0 & 2.0 & 4.0 & 5.0 \\ 2.0 & 0 & 4.5 & 3.0 \\ 4.0 & 4.5 & 0 & 1.5 \\ 5.0 & 3.0 & 1.5 & 0 \end{array} \right ) \end{array}\] Consider clusters $A= \{ 1,2\}$ and $B = \{3,4\}$. Then using single linkage, \[\delta_{AB} = \delta_{24} = 3.0.\] Using complete linkage, \[\delta_{AB} = \delta_{14} = 5.0.\] Using average dissimilarity, \[\delta_{AB} = 2^{-1} \times 2^{-1} ( 4.0 + 5.0 + 4.5 + 3.0 ) = 4.125.\]

The R command to perform hierarchical clustering is

hclust(d.matrix, method=...)

where

d.matrix is a dissimilarity matrix.
method can be single, complete or average (amongst others).

The output from the analysis is the set of clusters at each iteration, and the dissimilarity level at which the clusters formed. This can be neatly displayed as a dendrogram – see Example 7.2.

Example 7.2 Cluster Analysis for US Republican Voting Data

The data set repub contained the percentage of the vote given to the republican candidate in American Presidential elections from 1916 to 1976 for a selection of states. Looking for clusters containing states with similiar voting patterns might be of potential interest to political analysts. We could start by using a star plot as an informal way to assess whether any clustering might be present. A star plot presents a 2-dimensional summary of a multivariate dataset by plotting variable values (normalized to lie between 0 and 1) as rays projecting from the star’s center. This technique allows for a quick comparison between individuals in a dataset, allowing one to see which individuals cluster together. Figure 7.1 is produced using stars(repub). It is quite easy to see that there are several very similar states (in terms of Republican voting). Notice the somewhat strange voting pattern in Mississippi, where the Republican vote is usually poor but there are some exceptional years (in comparison to other states).

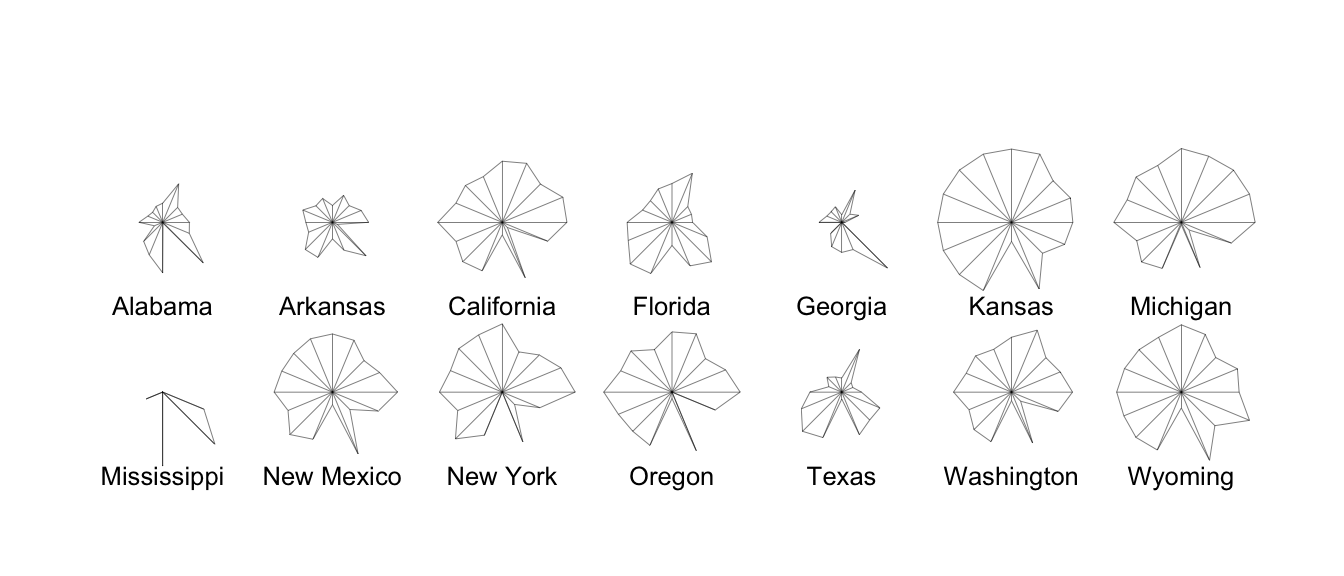
Figure 7.1: Stars plot for republican voting data.

Applying the hclust command, R code for producing a dendrogram to display hierarchical clustering is given below.

repub <- read_csv("../data/repub.csv") |>
  column_to_rownames("State")
repub.dist <- repub |> dist(method = "euclidean")
repub.clust.single <- repub.dist |> hclust(method = "single")
repub.clust.complete <- repub.dist |> hclust(method="complete")
library(ggdendro)
ggdendrogram(repub.clust.single)
ggdendrogram(repub.clust.complete)

Note that we use column_to_rownames() here to move the State column to the rownames. This is so that when we apply dist() to produce the distance matrix, the rows and columns are labelled. These labels are then kept through the hclust() functions. The ggdendrogram() function from the ggdendro package gives us ggplot2 consistent plotting.

The dendrograms produced are displayed in Figures 7.2 and 7.3. Note that the dissimilarity between two groups can be read off from the height at which they join. So, for example, with single linkage (in Figure 7.2 the group $\{ \textsf{Alabama}, \textsf{Georgia} \}$ and the group $\{ \textsf{Arkansas}, \textsf{Florida}, \textsf{Texas} \}$ join at a dissimilarity of about 38. (In fact, the exact figure is $37.79937$ which can be obtained by inspecting repub.clust.single$height).

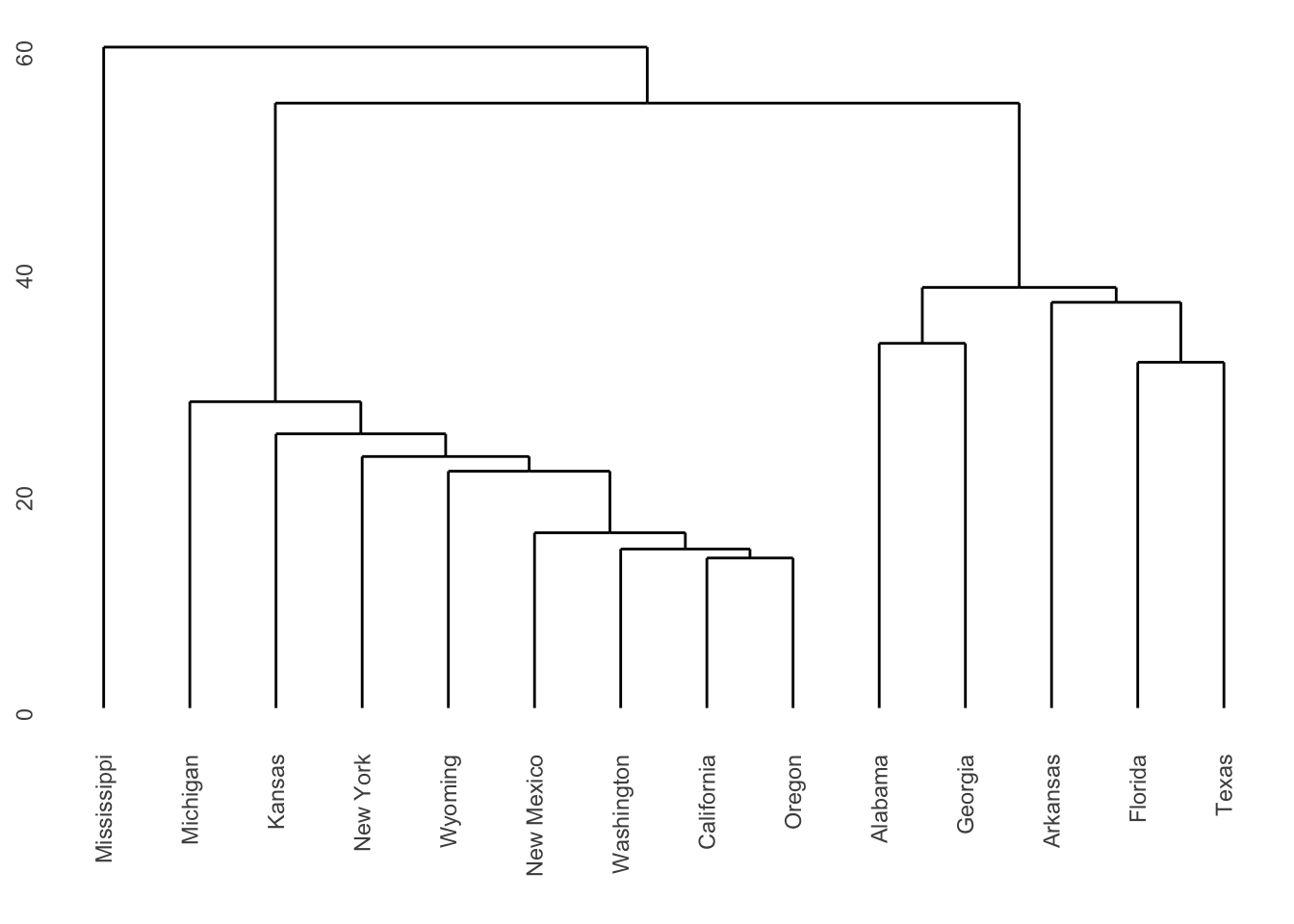
Figure 7.2: Dendrogram for Republican voting data, obtained using single linkage.

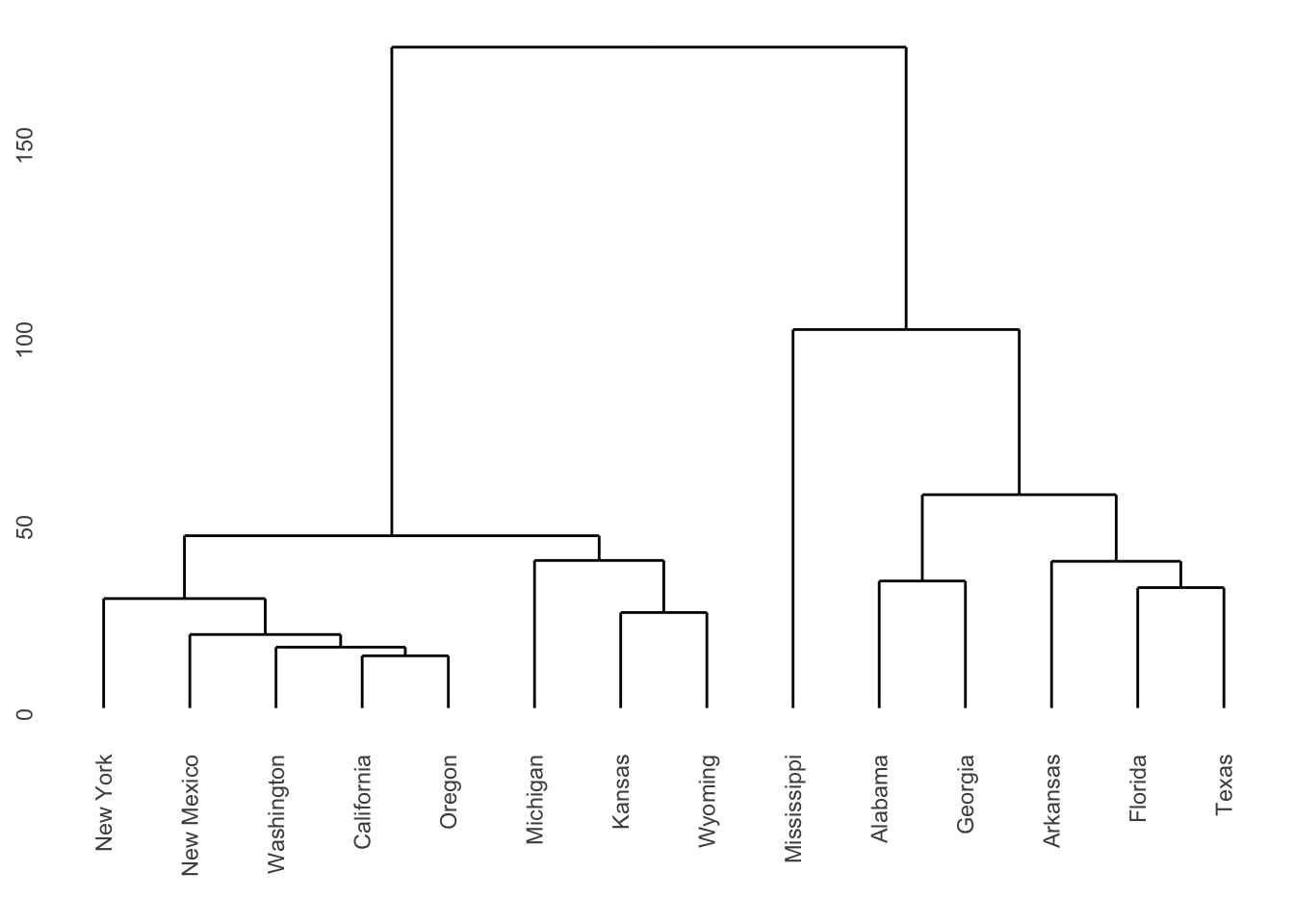
Figure 7.3: Dendrogram for Republican voting data, obtained using complete linkage.

Note that a dendrogram does not define a unique set of clusters. If the user wants a particular set of clusters, then these can be obtained by ‘cutting’ the dendrogram at a particular height, and defining the clusters according to the groups which formed below that height. For instance, if we use a cut-off height of 75 with complete linkage then three clusters emerge:

Cluster 1: New York, New Mexico, Washington, California, Oregon, Michigan, Kansas, Wyoming.
Cluster 2: Mississippi.
Cluster 3: Alabama, Georgia, Arkansas, Florida, Texas.

These groupings were obtained by inspection of the dendrogram. Such a process would clearly have been laborious had all 50 states been present in the data. Fortunately the R command cutree generates group membership automatically.

repub.groups.complete <- repub.clust.complete |> cutree(h=75)
repub.groups.complete

#>     Alabama    Arkansas  California     Florida     Georgia      Kansas 
#>           1           1           2           1           1           2 
#>    Michigan Mississippi  New Mexico    New York      Oregon       Texas 
#>           2           3           2           2           2           1 
#>  Washington     Wyoming 
#>           2           2

Single and Complete Linkage Compared

Single linkage is prone to ‘chaining’. In the figure below the three groups on the right will merge together (in a kind of chain) before combining with the group on the left. Note that everything would change if a single datum were added midway between the two groups on the left – these groups would then combine earlier than those on the right. This can be viewed as an unwanted lack of robustness with single linkage.

The central cluster in Figure 7.2 in Example 7.2 shows an instance of chaining with real data.
The growth of large clusters at small heights is very unlikely under complete linkage. In the figure below the middle cluster will combine with the right hand cluster because the extreme left hand edge of the large left cluster is distant. Nonetheless, one’s intuitive feel is that the middle cluster should first combine with left hand cluster.

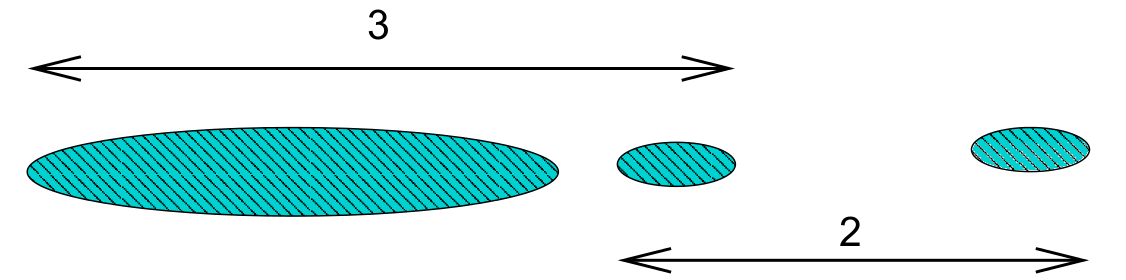
7.3 K-means clustering

If we have some knowledge apriori of the number of clusters $K$, then the problem of clustering changes to assigning each datum to a cluster such that within-cluster variation is minimized (and between-cluster variation maximised).

A naive way to address this problem is to compute the within-cluster variation for all possible assignments the $n$ data points to $K$ clusters. We then pick the assignment with minimal variation. The problem is that the number of possible assignments is given by: \[S(n,K) = \frac{1}{K!}\sum_{k=1}^K (-1)^{K-k}\dbinom{K}{k}k^n.\] The leading term here is $\frac{K^n}{K!}$ which gets large very quickly as $n$ increases! We thus settle for an approximate solution via the iterative $K$-means algorithm.

For a set of $n$ numerical datapoints $x_i$, the average total variation in the data may be measured using \[T=\frac{1}{2N}\sum_{i=1}^n\sum_{j=1}^n d(x_i,x_j)\] where $d$ is the dissimilarity metric. If we denote $C(i)$ as the cluster that point $x_i$ is assigned to, we may re-write this as \[\begin{aligned} T &= \frac{1}{2N}\sum_{k=1}^K\sum_{C(i)=k}\left(\sum_{C(j)=k}d(x_i,x_j) + \sum_{C(j)\neq k}d(x_i,x_j)\right)\\ &= W(C) + B(C).\end{aligned}\] where $W(C)$ is the within-cluster variation \[W(C) = \frac{1}{2N}\sum_{k=1}^K\sum_{C(i)=k}\sum_{C(j)=k}d(x_i,x_j),\] and $B(C)$ is the between-cluster variation \[B(C) = \frac{1}{2N}\sum_{k=1}^K\sum_{C(i)=k}\sum_{C(j)\neq k}d(x_i,x_j).\] Noting that $T$ is a constant, minimizing $W(C)$ is equivalent to maximising $B(C)$.

If $d(x_i,x_j)$ is the Euclidean distance, then these simplify to \[\begin{aligned} W(C) &= \sum_{k=1}^K \sum_{C(i)=k} (x_i - \mu_k)^2,\\ B(C) &= \sum_{k=1}^K N_k (\mu_k - \mu)^2,\\\end{aligned}\] where $N_k$ is the number of data points in cluster $k$, $\mu_k$ is the mean of the data points in cluster $k$, and $\mu$ is the mean of all datapoints (grand mean).

This gives us the basis of the $K$-means algorithm:

Start by placing the cluster means $\mu_k$ arbitrarily.
Compute the cluster assignment by assigning each datapoint $x_i$ to the closest cluster mean: \[C(i) = \mathop{\mathrm{arg\,min}}_{1 \leq k \leq K} (x_i - \mu_k)^2.\]
Recompute the cluster means $\mu_k$.
Repeat from 1 until $\mu_k$ reach convergence.

Note the similarity with linear discriminant analysis: Rather than have a training data set define the cluster means and then assigning observations to the closest cluster, we use an iterative procedure where data from the previous iteration may be considered the training data.

There are a number of pros and cons to this method.

The algorithm is simple to implement, requiring only means and distances to be calculated.
The algorithm will always converge, but may only converge to a local minima rather than the global minimum⁶³.
It is restricted to numerical data.
As means are used (Euclidean distance), outliers may be problematic.
Requires apriori knowledge of the number of clusters $K$.

Example 7.3 $K$-means example on synthetic data

Given randomly generated data from 3 distributions in two-dimensions in Figure 7.4.

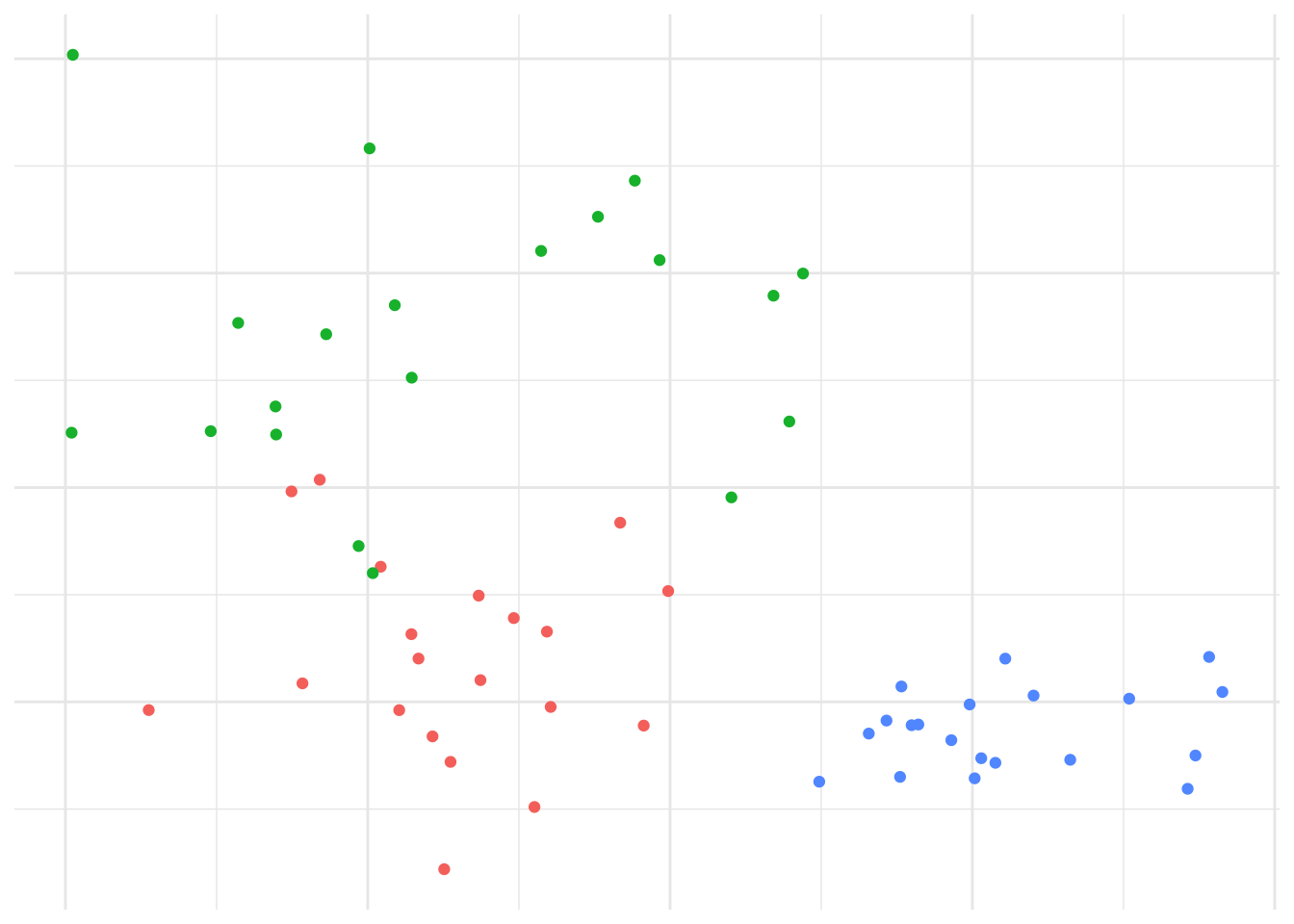
$Data generated from 3 distributions for Example \@ref(exm:kmeans).$

Figure 7.4: Data generated from 3 distributions for Example 7.3.

We’d expect that $K=3$ is reasonable, so let’s explore how the $K$-means algorithm operates: Figure 7.5 shows the initial (random) cluster means, and several further iterations of the algorithm. We seed the algorithm by sampling 3 points randomly from the data. Notice how with even relatively poor choices for the initial cluster means, the algorithm still correctly identifies the clusters in this case, and converges quite quickly: There’s very little difference in the cluster means after the 8th iteration. The similarity with linear discriminant analysis is seen here as well, in that you can imagine lines bisecting the midpoints of the pair-wise cluster means dividing the region into partitions that contain each cluster.

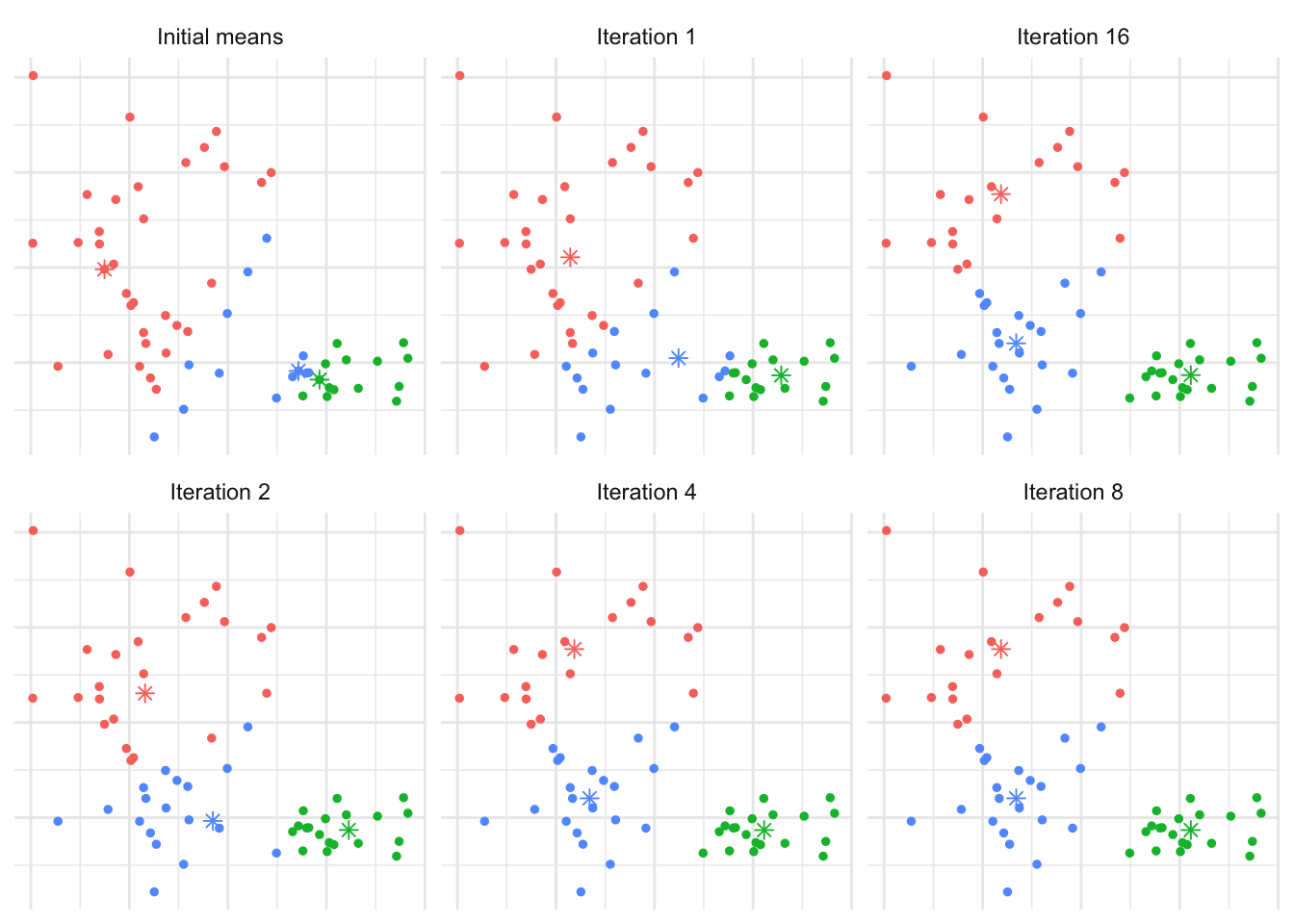
$The $K$-means algorithm in practice after several iterations for Example \@ref(exm:kmeans).$

Figure 7.5: The $K$-means algorithm in practice after several iterations for Example 7.3.

In order to find an appropriate value for $K$, one method is to apply the $K$-means algorithm for a number of different values for $K$, and compare the within cluster variance produced under each value. It’s clear that the within-cluster variance will decrease monotonically, so rather than looking for the smallest value we instead look to see which value of $K$ results in the largest decrease compared to $K-1$ - typically we’re looking for the ‘kink’ in the graph of the within cluster variance versus $K$. Figure 7.6 shows this for the above example. The majority of the reduction in cluster variance occurs by $K=3$, and while things continue to improve, the relative improvement is minor.

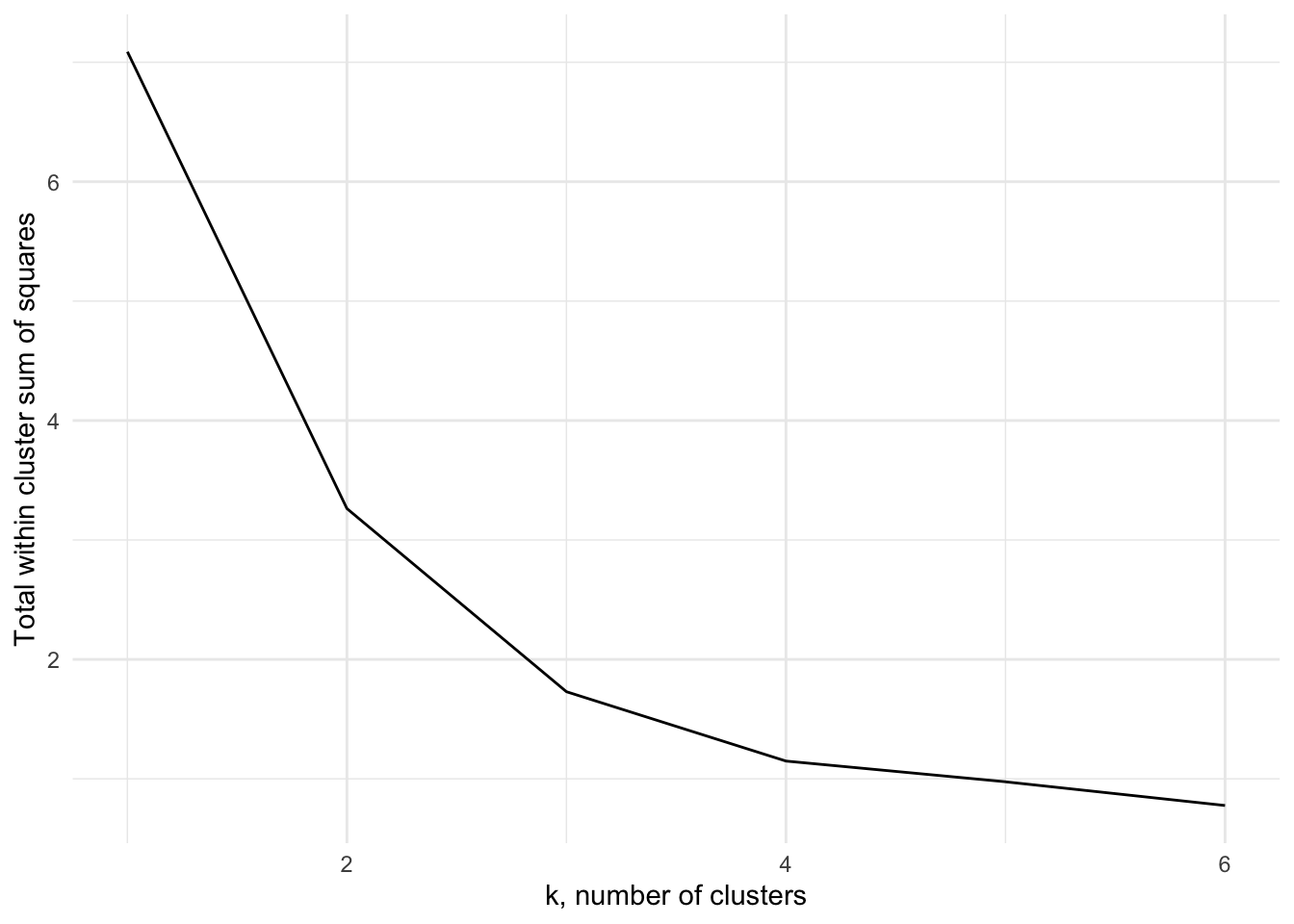
$The within cluster variance for one to six clusters for Example \@ref(exm:kmeans)$

Figure 7.6: The within cluster variance for one to six clusters for Example 7.3

The $K$-means algorithm is implemented using the kmeans function in R which has syntax

kmeans(x, centers, nstart = 1)

where x is the data, centers the number of clusters, and nstart may be optionally specifed to run the algorithm several times from different starting points, helping to minimise the chance of us being left with a local minima rather than the global minimum. The output class contains components

clusters: the cluster assignment for each observation.
centers: the center of each cluster.
withinss: the within cluster variation (sum of squares).
size: the size of each cluster.

The information can be extracted into tidy data frames using tidy(), augment() and glance() from the broom package in a similar way as we can extract information for linear models.

Example 7.4 $K$-means of Penguins from the Palmer Archipelago

These data consiste of measurements of size, clutch observations and blood isotope ratios for adult foraging Adélie, Chinstrap, and Gentoo penguins observed on islands in the Palmer Archipelago near Palmer Station, Antartica. Data were collected and made available by Dr Kristen Gorman and the Palmer Station Long Term Ecological Research (LTER) Program.

We’ll use the measurements flipper_length_mm, bill_length_mm and body_mass_g in order to cluster the penguins, under the assumption that we don’t know what the underlying species is, and see whether the $K$-means algorithm allows us to distinguish the species.

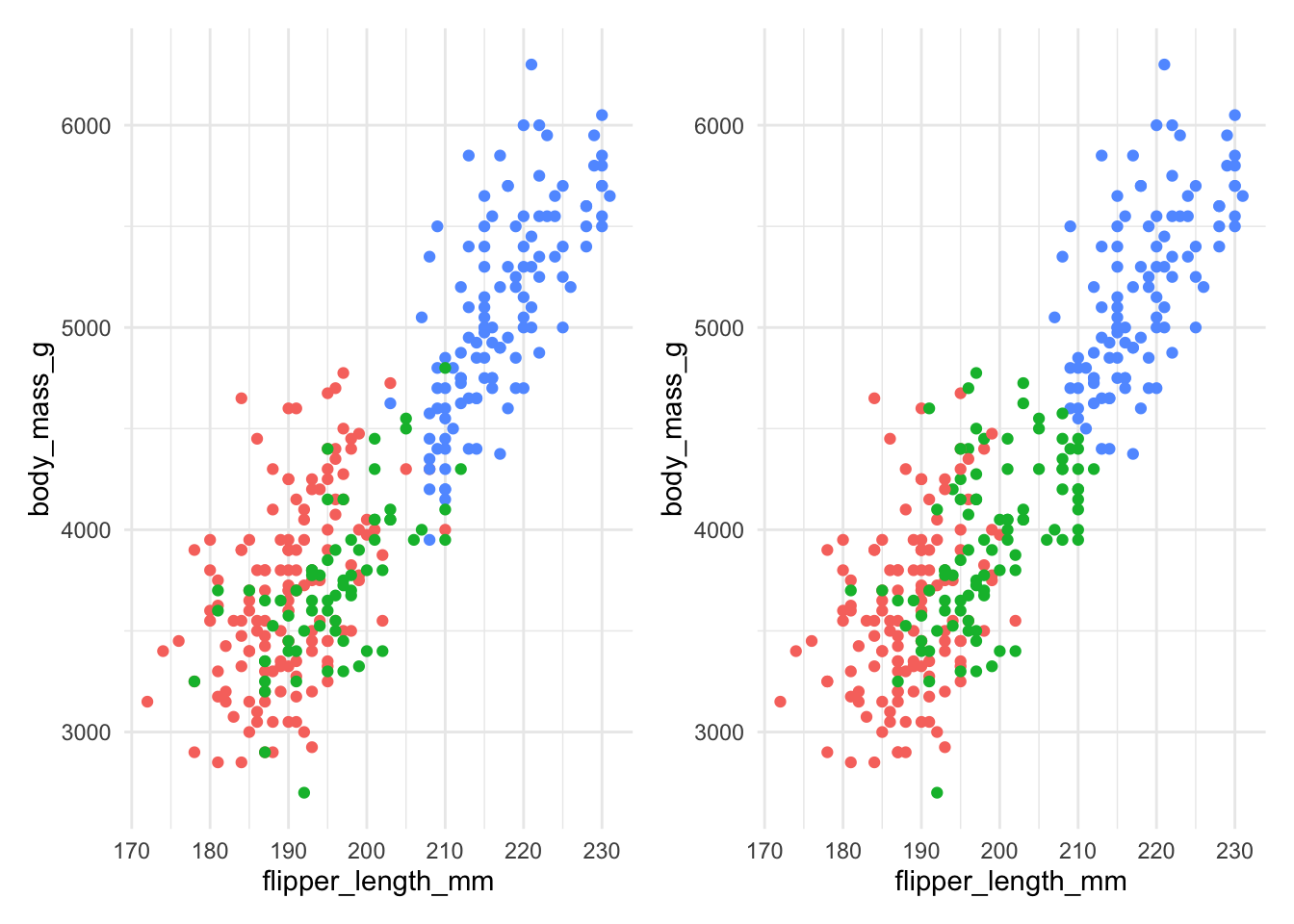
$The actual species (left) and clusters found using $K$-means with 3 clusters (right) for Example \@ref(exm:penguins).$

Figure 7.7: The actual species (left) and clusters found using $K$-means with 3 clusters (right) for Example 7.4.

Figure 7.7 compares the actual species (on the left) with the clusters found by the $K$-means algorithm on the right. We can see that the $K$-means algorithm does reasonably well, though there is some incorrect allocation fo moderate flipper lengths and body masses. The code used is below:

ggplot(penguins) +
  geom_point(mapping=aes(x=flipper_length_mm,
                         y=body_mass_g,
                         col=species))

km <- penguins |>
  select(flipper_length_mm, bill_length_mm, body_mass_g) |>
  mutate(across(everything(), scale)) |>
  kmeans(centers=3, nstart=20)

km |> augment(penguins) |>
  ggplot() +
  geom_point(mapping=aes(x=flipper_length_mm,
                       y=body_mass_g,
                       col=.cluster))

Notice that we’re specifying nstart=20 when using kmeans. This requests that the $K$-means algorithm is run using 20 separate starting cluster positions, helping to minimise the chance of us being left with a local minima rather than the global minimum. We’re also scaling each predictor (via the mutate function) to a common scale to ensure that all the variables were on the same scale. If we don’t do that, we’d end up with body_mass_g dominating, as shown in Figure 7.8

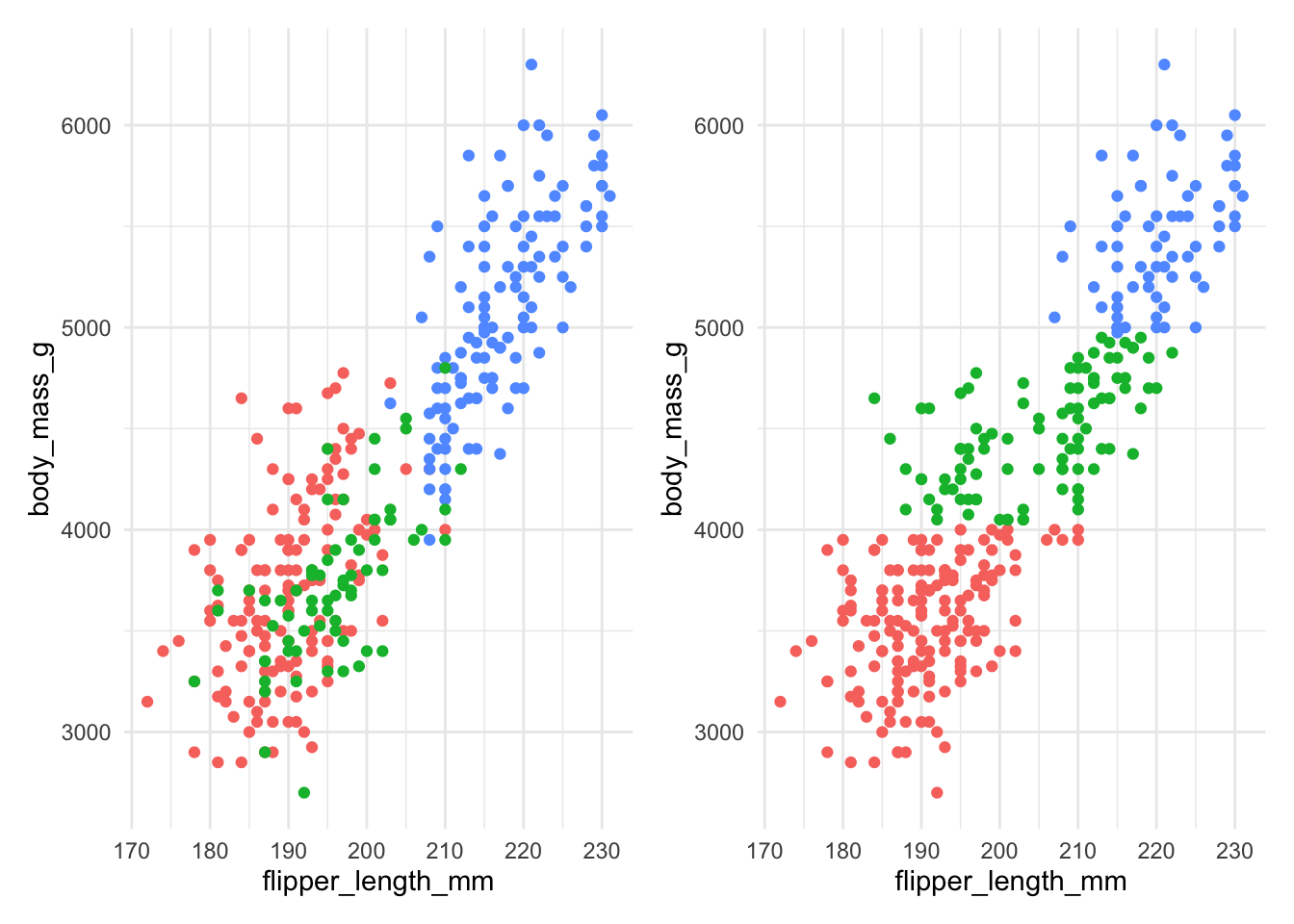
$The actual species (left) and clusters found using $K$-means with 3 clusters (right) for Example \@ref(exm:penguins) without scaling.$

Figure 7.8: The actual species (left) and clusters found using $K$-means with 3 clusters (right) for Example 7.4 without scaling.

Figure 7.8 shows that without scaling, the division into clusters happens almost exclusively along the body_mass_g axis, as this contributes the most to the distance between observations. This clearly gives a clustering that does not align well at all to the actual species.

Figure 7.9 compares the total within cluster sum of squares for a range of $k$ for scaled (left) and unscaled (right) data. We see in either case that the data suggest that two clusters may be best, though the scaled data does show a very slightly larger kink at 3 clusters.

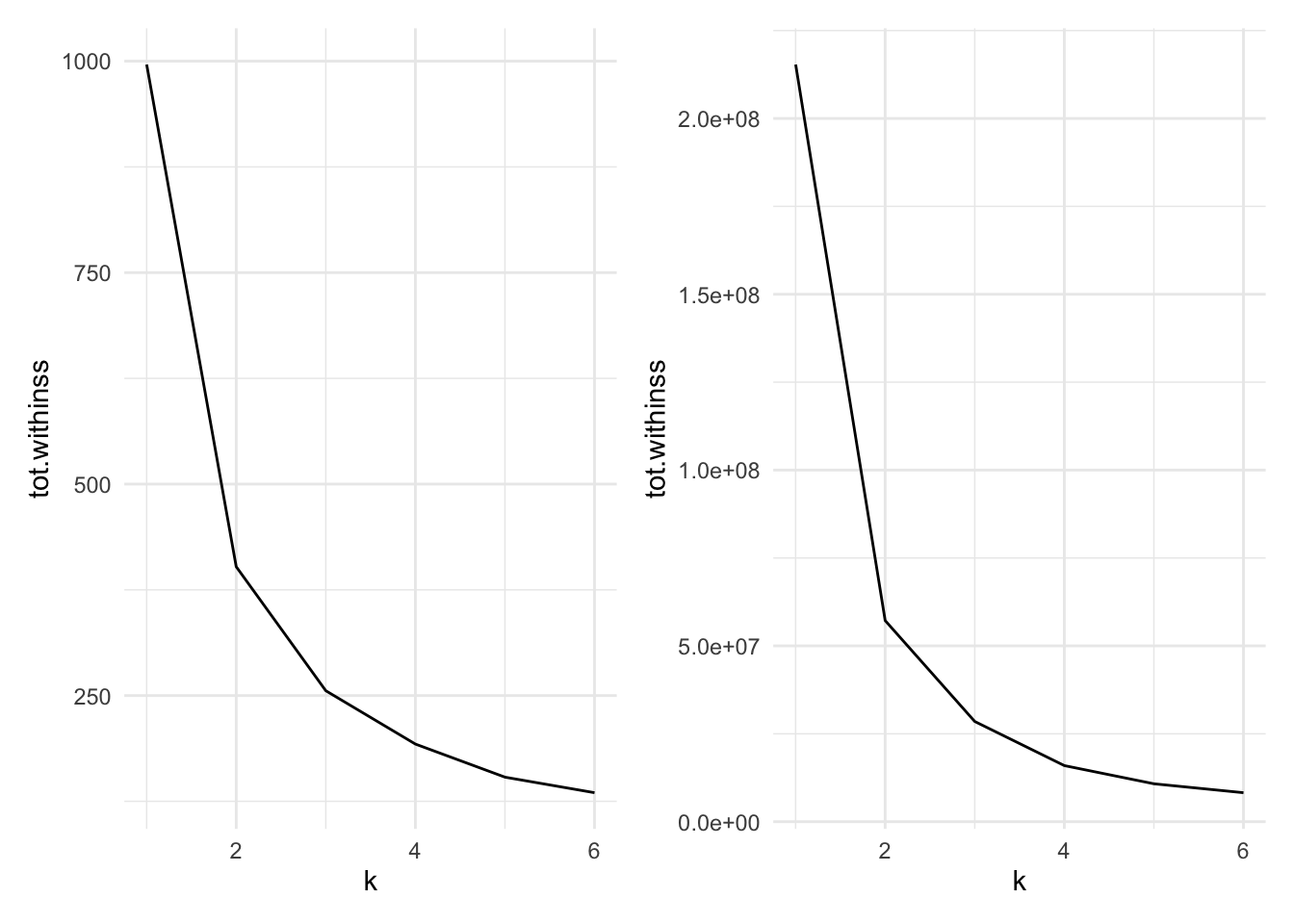
$Cluster size versus within cluster variation for Example \@ref(exm:penguins). Scaled data left, unscaled data right$

Figure 7.9: Cluster size versus within cluster variation for Example 7.4. Scaled data left, unscaled data right

The code to produce the datasets for these charts is below:

peng.scale <- penguins |>
  select(flipper_length_mm, bill_length_mm, body_mass_g) |>
  mutate(across(everything(), scale))

peng_ss <- tibble(k=1:6) |>
  mutate(
    km = map(k, ~ kmeans(peng.scale, centers=., nstart=20)),
    tidied = map(km, glance)
  ) |>
  unnest(tidied)
peng_ss

We scale the penguin data before applying kmeans.
To run kmeans across a range of k, we utilise the purrr package’s map function for applying a function across the list of k. This takes in a list (or vector) and operates a function on each entry in turn, returning a list.
The tibble(k=1:6) sets up a data.frame with a single column k ranging from one to six.
The mutate() command first uses map() to run the function kmeans() for each k on the scaled penguin data. Note that the varying parameter (k) in the map() is being passed in using the . argument - i.e. it is being mapped to the centers argument. The result of this will be a list column km, where each entry is an R object (in this case one of class kmeans).
The second line in mutate() then operates on the km list column, running the glance() command from broom which will return a tidy data.frame containing summary model fit information such as the sum of squares. this is then stored in the list column tidied.
Finally, we use unnest() from tidyr to expand the data.frames stored in the list column tidied, flattening them out so that each of the columns within tidied becomes a column in the main data frame.
In the end, we have columns for k, a list column km (storing the kmeans output), then the columns that result from the glance() function (totss the total sum of squares; tot.withinss, the total within-cluster sum of squares; betweenss, the between-cluster sum of squares; and iter, the number of iterations to convergence). As this is a tidy data.frame, it can be fed into ggplot() for plotting.

Example 7.5 $K$-means for image compression

One use of $K$-means (or any clustering method) is in image compression. Given an image, a simple way to compress the image is to replace each pixel (which is normally represented using 4 bytes) with an index into a smaller colour palette. If we can replace all the pixels in the image with just 16 colours for example, each pixel would then take up just 0.5 bytes, a compression ratio of 1:8. Replacing arbitrary colours by a small set is exactly the problem that clustering is attempting to solve. It works best on images that have few colour gradients, rather than on images with lots of subtle colour differences. Figure 7.10 shows the same image clustered using a range of colours.

The same image clustered using top, from left: 2, 4, 8 colours and bottom from left: 16, 32, 256 colours.

Figure 7.10: The same image clustered using top, from left: 2, 4, 8 colours and bottom from left: 16, 32, 256 colours.

7.4 K-medoids clustering

So far we have used only the Euclidean distance as our dissimilarity measure. The Euclidean distance is not appropriate, however, if we have categorical data, or the data are on very different scales. Instead, the $K$-mediods algorithm may be used which uses only the distances between data points, allowing any dissimilarity matrix to be used. The algorithm is as follows:

Pick initial data points to be cluster centers $m_k$.
Compute the cluster assignment by assigning each datapoint $x_i$ to the closest cluster center. \[C(i) = \mathop{\mathrm{arg\,min}}_{1 \leq k \leq K} d(x_i, m_k).\]
Find the observation in each cluster that minimises the total distance to other points in that cluster. \[i_k = \mathop{\mathrm{arg\,min}}_{C(i)=k} \sum_{C(j)=k} d(x_i, x_j).\]
Assign $m_k = x_{i_k}$.
Repeat from 1 until the $m_k$ reach convergence.

This is significantly more costly than $K$-means as we have lost the simplification of using the means of each cluster as the center. The pam function (Partitioning Around Medoids) in the cluster package may be used to compute the $K$-medoids of a dataset. Like hclust, it can take a dissimilarity object directly, thus overcoming the restriction of utilising only the Euclidean distance function. The syntax is

pam(x, k, metric = "euclidean")

where x is either a data frame or a dissimilarity matrix, k is the number of clusters. metric specifies the dissimilarity measure to use in the case x is a data frame.

Example 7.6 $K$-medoids to Republican voting data

We show how to use the pam function on the US republican voting data from example 7.2.

library(cluster)
pam(repub, k=3, metric="manhattan")

#> Medoids:
#>             ID  1916  1920  1924  1928  1932  1936  1940  1944  1948  1952
#> Arkansas     2 28.01 38.73 29.28 39.33 12.91 17.86 20.87 29.84 21.02 43.76
#> California   3 46.26 66.24 57.21 64.70 37.40 31.70 41.35 42.99 47.14 56.39
#> Mississippi  8  4.91 14.03  7.60 17.90  3.55  2.74  4.19  6.44  2.62 39.56
#>              1956  1960 1964 1968 1972  1976
#> Arkansas    45.82 43.06 43.9 30.8 68.9 34.97
#> California  55.40 50.10 40.9 47.8 55.0 50.89
#> Mississippi 24.46 24.67 87.1 13.5 78.2 49.21
#> Clustering vector:
#>     Alabama    Arkansas  California     Florida     Georgia      Kansas 
#>           1           1           2           1           1           2 
#>    Michigan Mississippi  New Mexico    New York      Oregon       Texas 
#>           2           3           2           2           2           1 
#>  Washington     Wyoming 
#>           2           2 
#> Objective function:
#>    build     swap 
#> 82.00643 74.48071 
#> 
#> Available components:
#>  [1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
#>  [6] "clusinfo"   "silinfo"    "diss"       "call"       "data"

As with kmeans, we can clean up this output using tidy() to extract the medoids, glance() to extract the model fit information, and augment() to add the clustering information to the original data.

Here we’ve used the Manhattan distance as opposed to the Euclidean distance, yet we’ve retreived the same grouping as we did in example 7.2, with Mississippi being in a cluster on it’s own, and the other states grouping into two clusters. We could also do this using some other distance measures, by passing the dissimilarity object into pam instead of the data frame.

repub.dist <- dist(repub, method="manhattan")
pam(repub.dist, k=3)

#> Medoids:
#>      ID               
#> [1,] "2" "Arkansas"   
#> [2,] "3" "California" 
#> [3,] "8" "Mississippi"
#> Clustering vector:
#>     Alabama    Arkansas  California     Florida     Georgia      Kansas 
#>           1           1           2           1           1           2 
#>    Michigan Mississippi  New Mexico    New York      Oregon       Texas 
#>           2           3           2           2           2           1 
#>  Washington     Wyoming 
#>           2           2 
#> Objective function:
#>    build     swap 
#> 82.00643 74.48071 
#> 
#> Available components:
#> [1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
#> [6] "clusinfo"   "silinfo"    "diss"       "call"

7.5 Silhouette plots

We’ve already mentioned one heuristic that can be used to determine the most appropriate number of clusters for the data. Another technique is to use a silhouette plot which is produced using the cluster package.

Given a clustering, the silhouette $s(i)$ of an observation $x_i$ is a measure of how well $x_i$ fits into the cluster to which it has been assigned, compared with the other clusters. It is computed using \[s(i) = \frac{b(i) - a(i)}{\max\{a(i),b(i)\} },\] where $a(i)$ is the average dissimilarity between $x_i$ and the rest of the points in the cluster to which $x_i$ belongs, and $b(i)$ is the smallest average dissimilarity between $x_i$ and the points in the other clusters⁶⁴. Figure 7.11 shows this diagramatically.

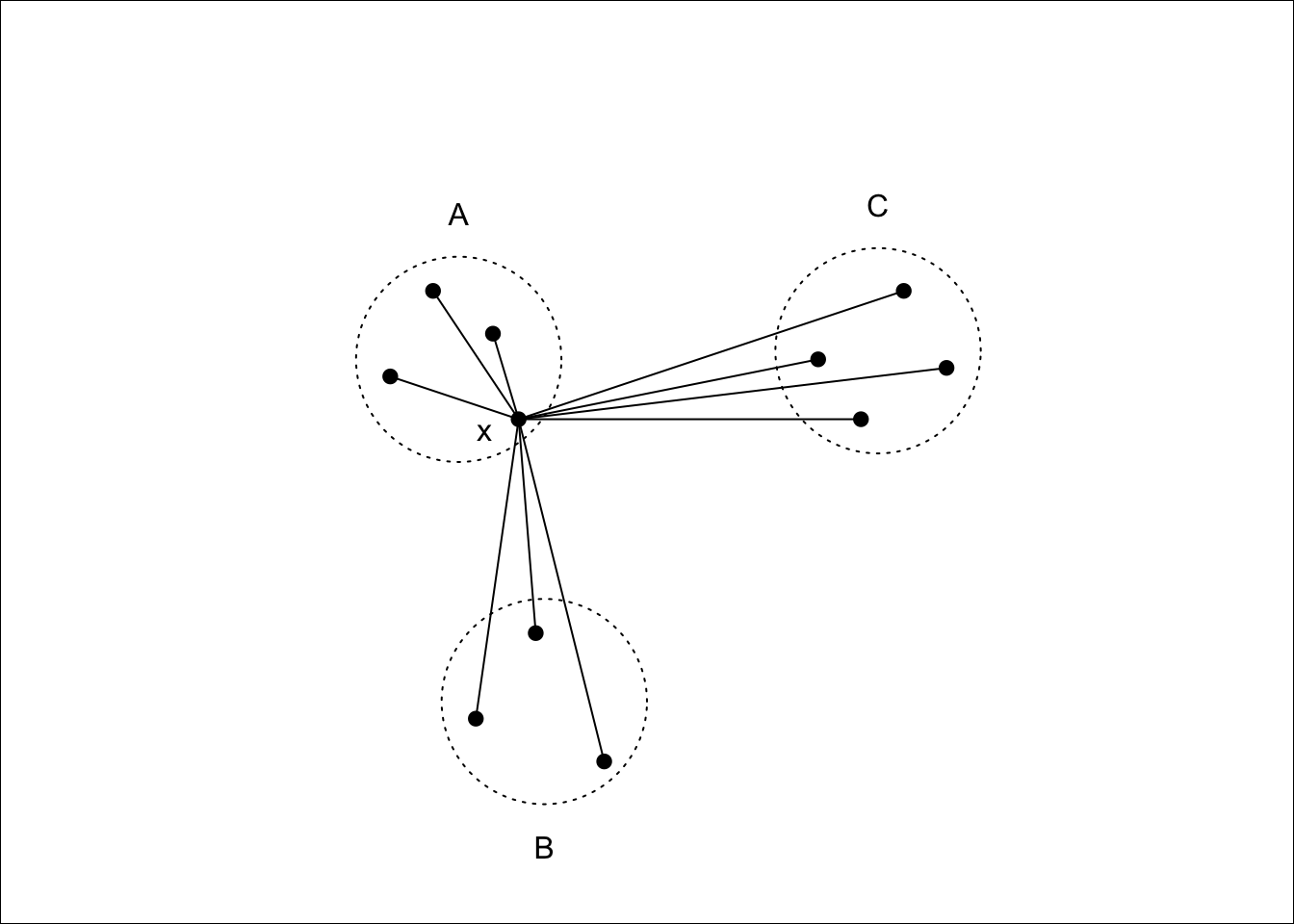
$x$ lies in cluster $A$, so $a(i)$ will be the average of the dissimilarities to other points in $A$. $b(i)$ will be the average dissimilarity to points in cluster $B$ as this is smaller than the average dissimilarity to cluster $C$.

Figure 7.11: $x$ lies in cluster $A$, so $a(i)$ will be the average of the dissimilarities to other points in $A$. $b(i)$ will be the average dissimilarity to points in cluster $B$ as this is smaller than the average dissimilarity to cluster $C$.

Notice that $s(i)$ can be at most $1$ when $a(i)$ is small compared to $b(i)$, suggesting that $x_i$ has been assigned to the correct cluster, as all other clusters are much further away. $s(i)$ can be as low as -1, however, when $b(i)$ is small compared to $a(i)$, which occurs if $x_i$ would be better suited in a different cluster. An $s(i)$ value of $0$ indicates that $x_i$ is equally close to two or more clusters.

A silhouette plot is a plot of the silhouettes of each observation, grouped by cluster, and sorted by decreasing silhouette. These plots give a visual indication of how the well clustered the data are: High silhouette values indicate well grouped clusters, with low silhouette values indicating clusters that are close to each other (which may suggest that they should be grouped together).

The average silhouette across all data may be used as a measure of how well clustered the data are. As the number of clusters increases, we would expect clustering to improve until a point is reached where a cluster is split into two or more clusters that remain close to one another (and thus not well grouped). Finding the number of clusters for which the average silhouette is maximised is often a reasonable heuristic for determining the appropriate number of clusters in a dataset.

A silhouette plot may be generated by using plot on a silhouette class, which can be generated from the output to pam, or by a dissimilarity matrix and a cluster vector. For the Republican voting data we have the following.

library(cluster)
repub.dist <- dist(repub, method="manhattan")
repub.pam.1 <- pam(repub.dist, k=3)
repub.pam.2 <- pam(repub.dist, k=4)
plot(silhouette(repub.pam.1), border=NA, do.clus.stat=FALSE, do.n.k=FALSE,
     main="3 clusters")
plot(silhouette(repub.pam.2), border=NA, do.clus.stat=FALSE, do.n.k=FALSE,
     main="4 clusters")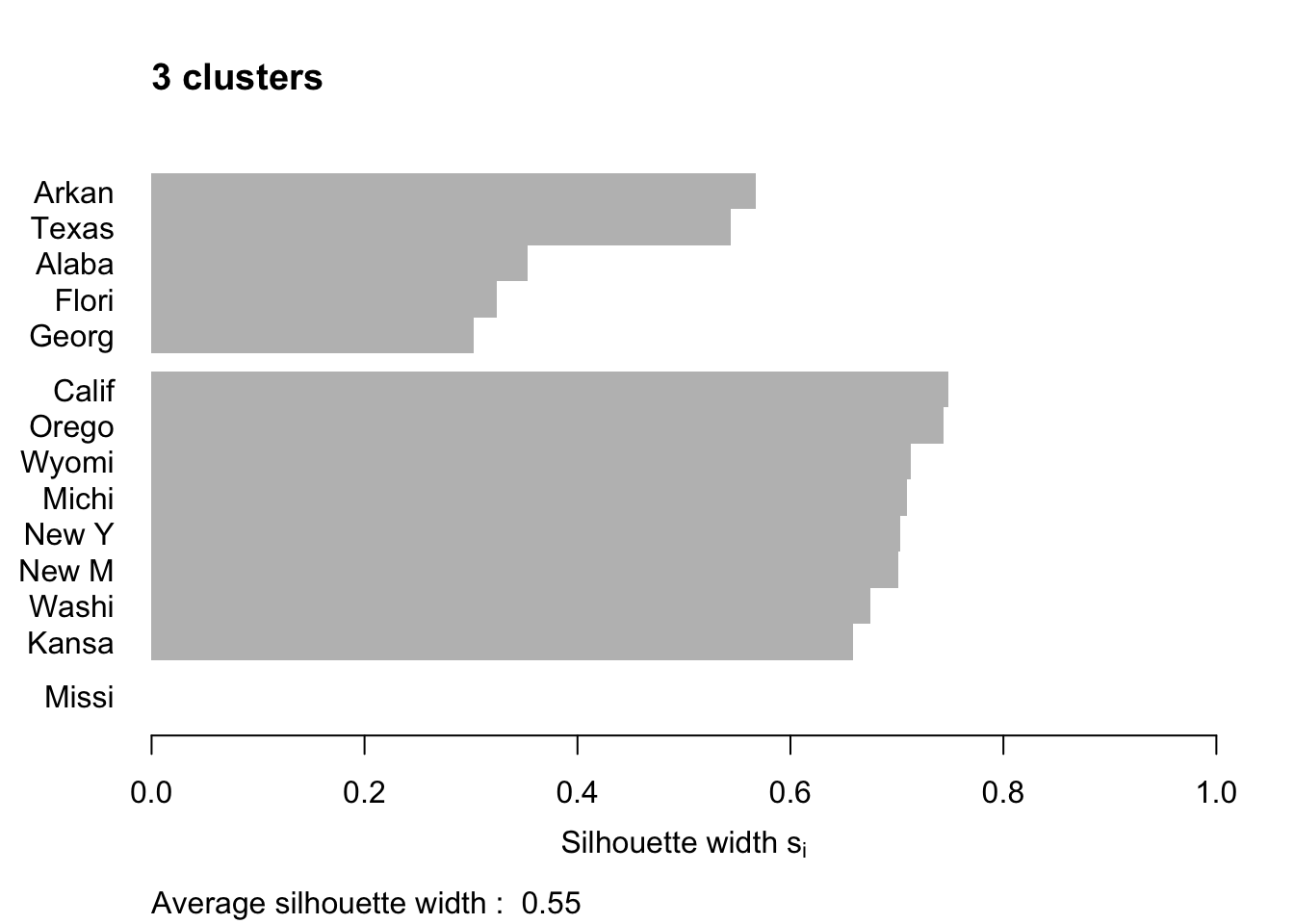

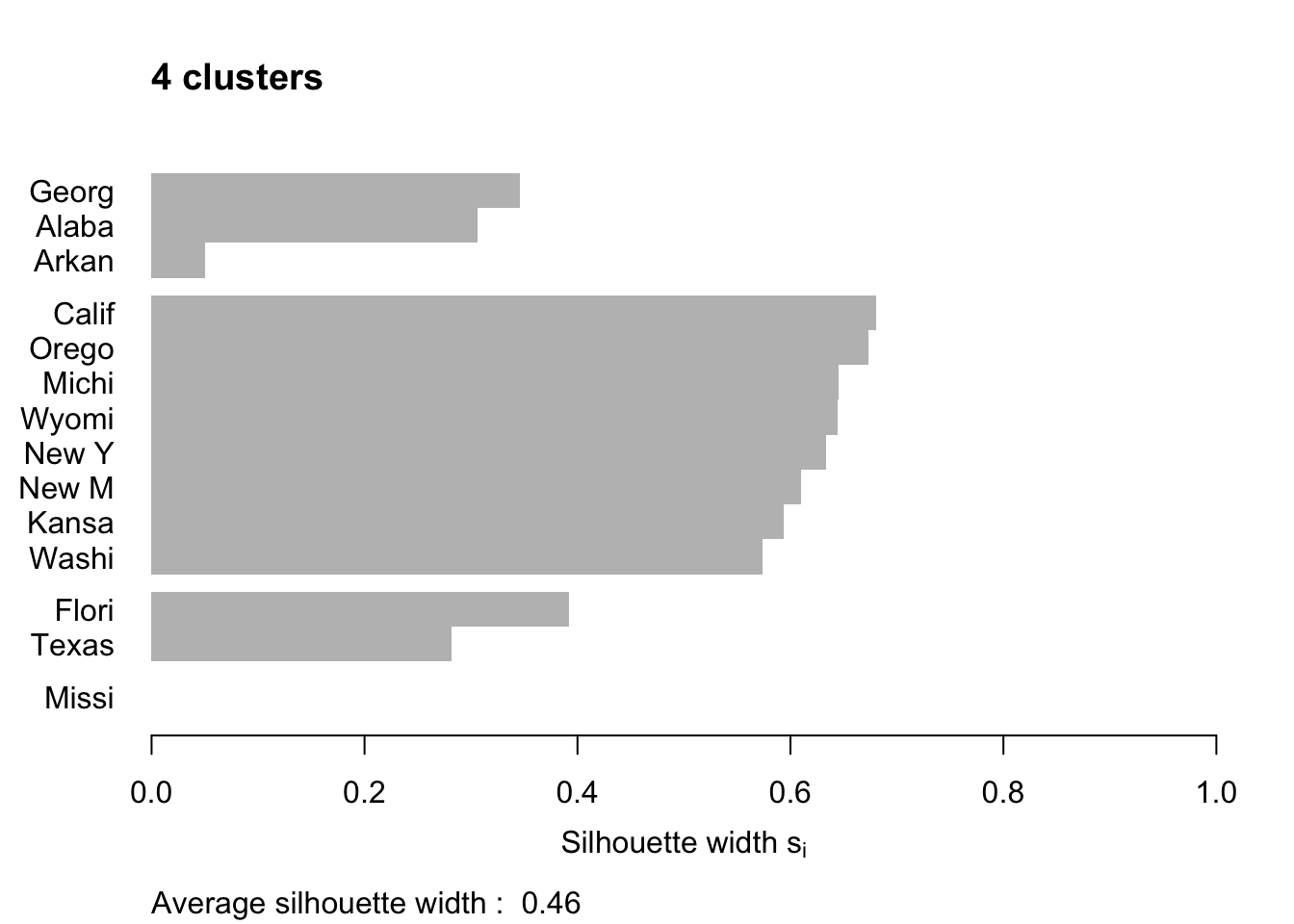
Figure 7.12: Silhouette plots of the republican voting data

Figure 7.12 shows the resulting plots. Points to note:

We have used border=NA to make sure the barplot that is produced has no border. This is important as the default plotting mode on Windows has no anti-aliasing enabled, which means transparent borders don’t correctly let the colour from the bars through so you end up with no bars. Setting the border to NA fixes this as it turns the border off.
We have used do.clus.stat=FALSE and do.n.k=FALSE to turn off some of the statistics that might otherwise crowd the plot. Experiment with these yourself.
The Mississippi silhouette is defined to be 1, as it is the only point in its cluster (and thus the average dissimilarity to other points in the cluster is not well-defined). To highlight this special-case, the silhouette bar has not been plotted.

There is a higher average silhouette for 3 clusters rather than 4, and some evidence in the 4 cluster silhouette plot that at least one of the clusters is not well grouped, with Arkansas having a low silhouette. Further information about this may be found by printing the silhouette output from the pam object:

repub.pam.2 |> pluck('silinfo', 'widths')

#>             cluster neighbor  sil_width
#> Georgia           1        3 0.34562691
#> Alabama           1        3 0.30613459
#> Arkansas          1        3 0.04979458
#> California        2        3 0.68012986
#> Oregon            2        3 0.67300077
#> Michigan          2        3 0.64554014
#> Wyoming           2        3 0.64475783
#> New York          2        3 0.63315168
#> New Mexico        2        3 0.60961094
#> Kansas            2        3 0.59358889
#> Washington        2        3 0.57341819
#> Florida           3        1 0.39220717
#> Texas             3        1 0.28198501
#> Mississippi       4        1 0.00000000

We can see that Arkansas lies between cluster 1 and cluster 3, perhaps suggesting that these two clusters may be artificially split.

If you wish to extract the silhouette information and plot yourself using ggplot2, you can do so via the pluck function above:

repub.pam.2 |> pluck('silinfo', 'widths') |>
  as.data.frame() |>
  rownames_to_column("State") |>
  ggplot() +
  geom_col(mapping = aes(y=as_factor(State), x=sil_width)) +
  labs(x="Silhouette width", y=NULL)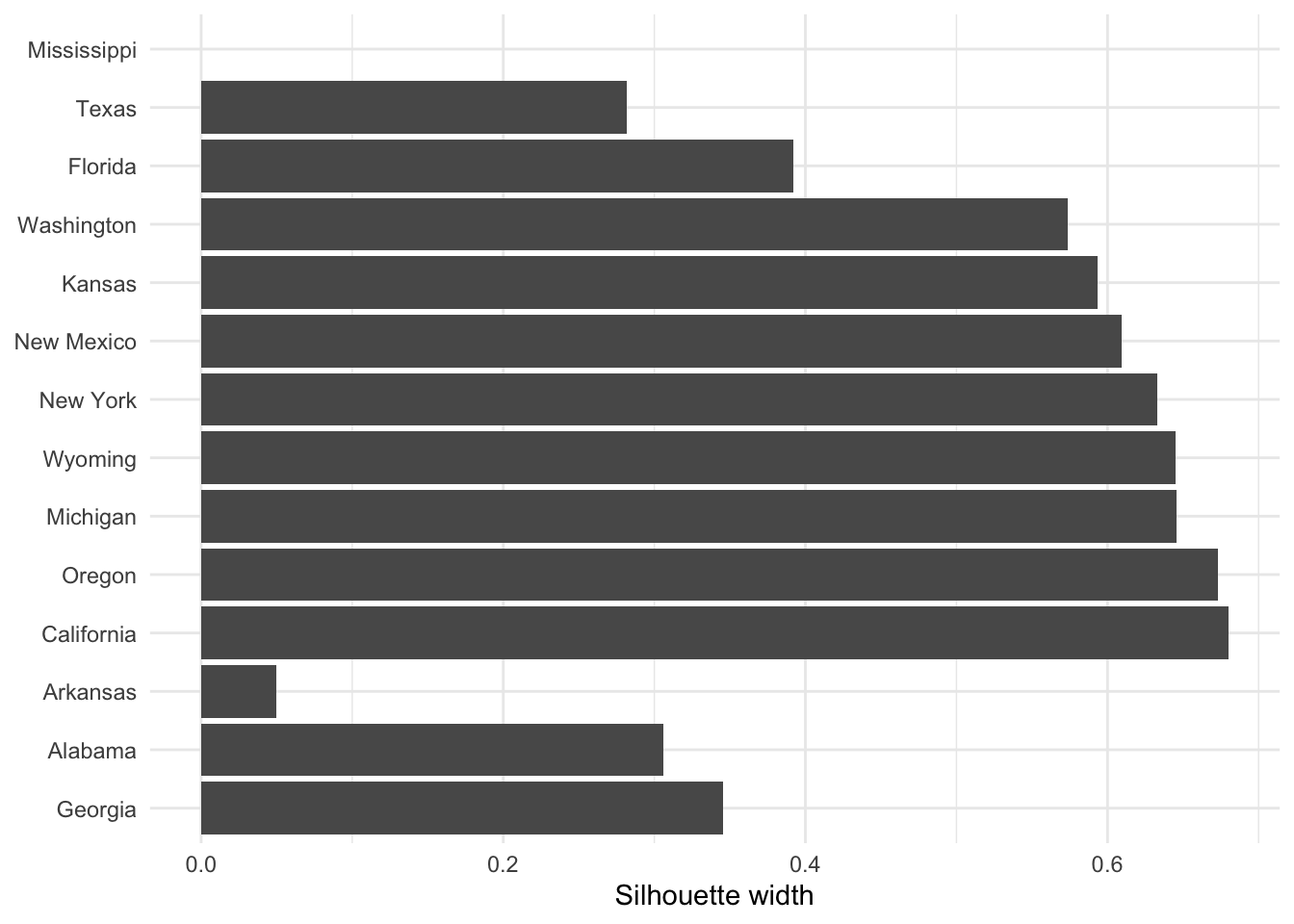

This can be useful for larger datasets, where you might like to just do a boxplot of the silhoutte widths for each cluster.

If you wish to generate a plot of silhouettes for output from kmeans or hclust you can use the second form of the silhouette command

silhouette(x, dist)

where x is a vector with the cluster numbers of each observation, such as clusters returned from kmeans or the output of cutree, and dist is a dissimilarity matrix, normally computed using dist. Note that you need not use the same dissimilarity measure as was used to generate the clustering. (e.g. the squared Euclidean measure used in kmeans). For the penguins data this may be done as follows.

set.seed(27)
peng.scaled <- penguins |>
  select(flipper_length_mm, bill_length_mm, bill_depth_mm, body_mass_g) |>
  mutate(across(everything(), scale))
peng.km.1 <- peng.scaled |> kmeans(centers=3, nstart=20)
peng.km.2 <- peng.scaled |> kmeans(centers=4, nstart=20)
peng.dist <- peng.scaled |> dist(method='euclidean')
peng.sil.1 <- peng.km.1 |> pluck('cluster') |> silhouette(dist=peng.dist)
peng.sil.2 <- peng.km.2 |> pluck('cluster') |> silhouette(dist=peng.dist)
peng.sil <- bind_rows(
    peng.sil.1 |> as.data.frame() |> mutate(k='k=3'),
    peng.sil.2 |> as.data.frame() |> mutate(k='k=4')
  ) |>
  mutate(cluster = as.factor(cluster))

ggplot(peng.sil) +
  geom_boxplot(mapping = aes(x=cluster, y=sil_width)) +
  facet_wrap(vars(k), scales='free_x')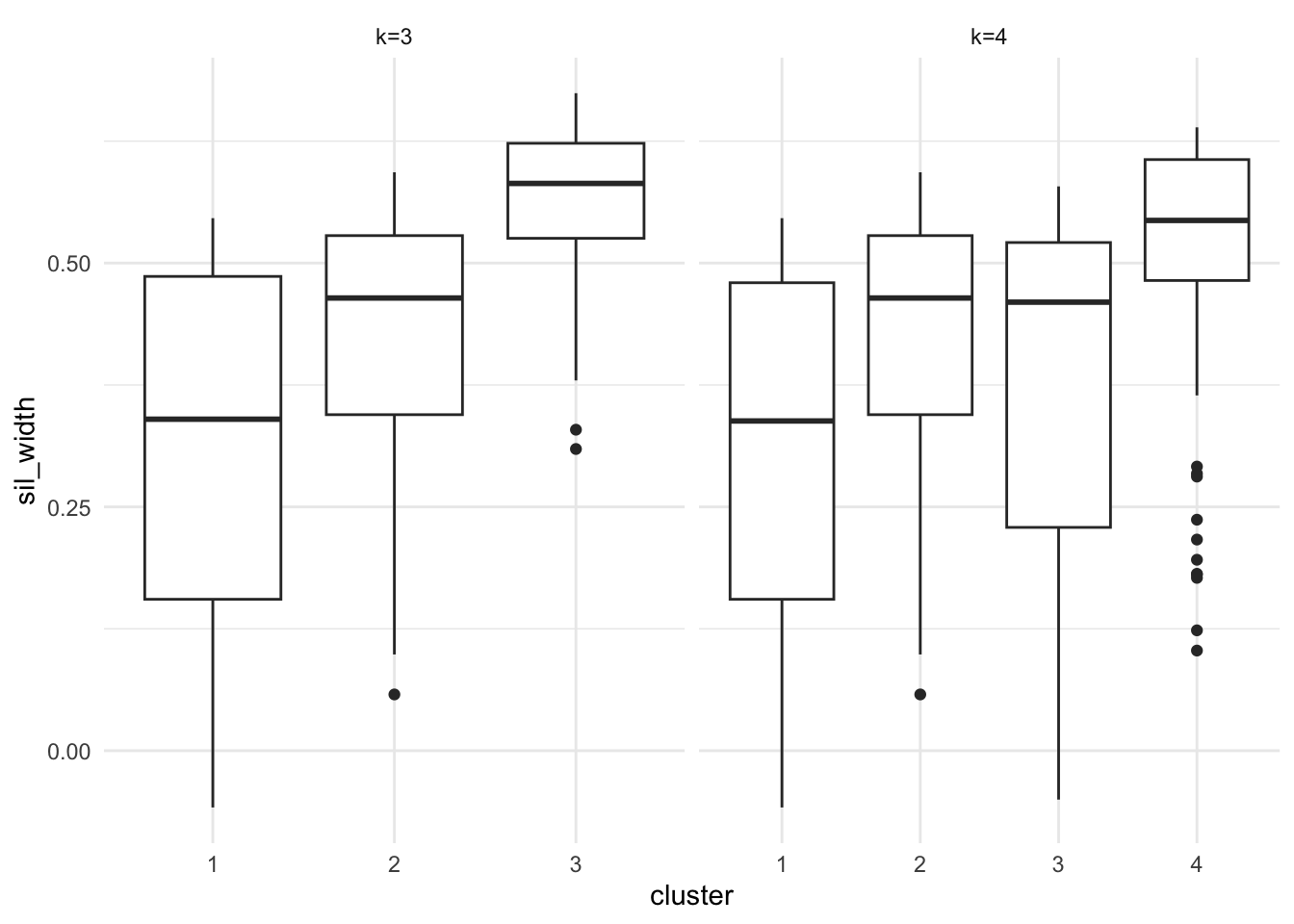

Figure 7.13: Silhouette plots of the Palmer Penguins data set

Plots are given in Figure 7.13. Points to note:

We’ve scaled the penguins data prior to fitting k-means or computing distances.
The silhouette() command utilises the cluster vector from the peng.km.1 object, so we’ve used pluck() to pull it out.
The silhouette() function returns a matrix with class silhouette. We coerce this into a data.frame for plotting.
We bind the two datasets together so we can plot them side by side with facetting.
We’ve used boxplots here rather than a standard silhouette plot, just by way of demonstration.
It is clear that the third cluster in the 3-cluster case has been split in two (clusters 3 and 4) in the 4-cluster case, each of which has lower average silhouette, suggesting this split is artificial.
Notice in both plots there are points with negative silhouettes. This suggests that these penguins may be better suited in one of the other clusters. Whilst the $k$-means algorithm has assigned these observations to the closest cluster based on the cluster centroid, that doesn’t necessarily mean that it is closest to all the points in that cluster. The different ways of measuring how close a point is to each cluster (e.g. cluster centroid versus average dissimilarity to other points in the cluster) may give different results, in the same way that single and complete linkage give different results in heirarchical clustering.

In fields such as computer science and image analysis, cluster analysis is referred to as unsupervised learning and discriminant analysis is referred to as supervised learning.↩︎
One potential way to avoid local minima is to start with a number of different initial cluster mean positions and pick the result that gives smallest within-cluster variation.↩︎
If a cluster contains only one point, the average dissimilarity to other points in the cluster is not well defined. We use the natural definition that $a(i)\equiv 0$ which gives $s(i)=1$ in this case.↩︎